(本小题满分12分) 过椭圆 的左顶点A做斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知
的左顶点A做斜率为2的直线,与椭圆的另一个交点为B,与y轴的交点为C,已知 .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设动直线y=kx+m与椭圆有且只有一个公共点P,且与直线x=4相交于点Q,若x轴上存在一定点
M(1,0),使得PM⊥QM,求椭圆的方程.
(本小题10分)函数 是偶函数.
是偶函数.
(1)求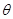 ;
;
(2)将函数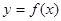 的图像先纵坐标不变,横坐标缩短为原来的
的图像先纵坐标不变,横坐标缩短为原来的 倍,再向左平移
倍,再向左平移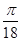 个单位,然后向上平移1个单位得到
个单位,然后向上平移1个单位得到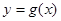 的图像,若关于
的图像,若关于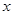 的方程
的方程 有且只有两个不同的根,求
有且只有两个不同的根,求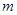 的范围.
的范围.
(本小题10分)如图,在平面直角坐标系xoy中,以ox轴为始边做两个锐角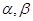 ,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为
,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为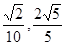
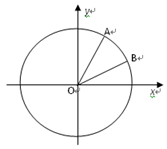
(1)求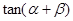 的值; (2)求
的值; (2)求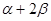 的值。
的值。
(本小题10分)已知函数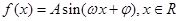 其中
其中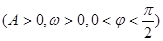 的周期为
的周期为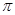 ,且图像上一个最高点为
,且图像上一个最高点为
(1)求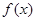 的解析式; (2)当
的解析式; (2)当 时,求
时,求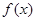 的值域.
的值域.
(本题10分)已知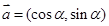 ,
,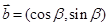 ,其中
,其中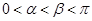 .
.
(1)求证: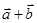 与
与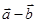 互相垂直;
互相垂直;
(2)若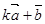 与
与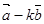 的长度相等,求
的长度相等,求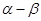 的值(
的值(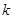 为非零的常数).
为非零的常数).
(本题10分)
(1)化简 ;
;
(2)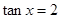 ,(1)求
,(1)求 的值。
的值。