(本小题10分)已知函数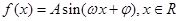 其中
其中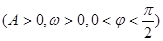 的周期为
的周期为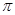 ,且图像上一个最高点为
,且图像上一个最高点为
(1)求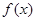 的解析式; (2)当
的解析式; (2)当 时,求
时,求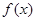 的值域.
的值域.
已知函数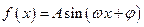
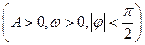 的部分图象如图所示
的部分图象如图所示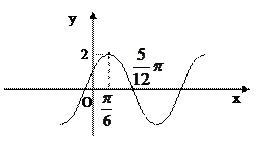 (1)求函数
(1)求函数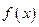 的解析式;
的解析式;
(2)如何由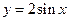 的图象通过
的图象通过
适当的变换得到函数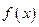 的
的
图象,写出变换过程。
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从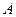 、
、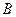 、
、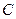 三个区中抽取7个工厂进行调查,已知
三个区中抽取7个工厂进行调查,已知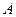 、
、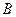 、
、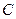 区中分别有18、27、18个工厂。
区中分别有18、27、18个工厂。
(1)求从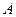 、
、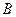 、
、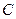 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(2)若从抽得的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自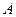 区的概率。
区的概率。
若对于一切实数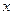 、
、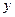 ,都有
,都有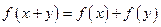
(1)求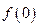 并证明
并证明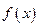 为奇函数;
为奇函数;
(2)若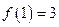 ,求
,求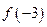 。
。
( 本小题满分16分)
本小题满分16分)
设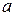 为实数,函数
为实数,函数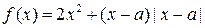 .
.
(1)若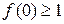 ,求
,求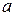
 的
的 取值范围;
取值范围;
(2)求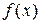 的最小值;
的最小值;
(3)设函数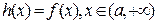 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式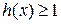 的解集.
的解集.
(本小题满分12分)
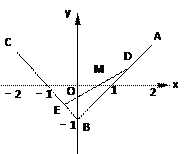
如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.