(本小题满分12分)
如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足="t," =" t" ,
="t" , t∈[0,1].
(Ⅰ) 求动直线DE斜率的变化范围;
(Ⅱ) 求动点M的轨迹方程.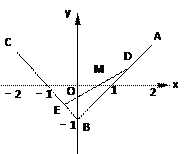
(本小题满分12分)已知:过抛物线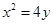 的焦点
的焦点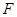 的直线交抛物线于
的直线交抛物线于 两个不同的点,过
两个不同的点,过 分别作抛物线的切线,且二者相交于点
分别作抛物线的切线,且二者相交于点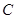

(1)求证: ;
;
(2)求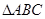 的面积的最小值。
的面积的最小值。
(本小题满分12分)在三棱锥 中,
中,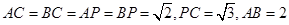 。
。
(1)求证: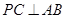 ;
;
(2)求二面角 的余弦值的绝对值。
的余弦值的绝对值。
(本小题满分12分)为了解甲、乙两厂的产品质量,分别从两厂生产的产品中各随机抽取10件,测量产品中某种元素的含量(单位:毫克),其测量数据的茎叶图如下: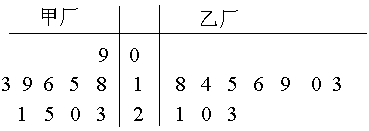
规定:当产品中此种元素含量大于18毫克时,认定该产品为优等品。
(1)试比较甲、乙两厂生产的产品中该种元素含量的平均值的大小;
(2)从乙厂抽出上述10件产品中,随机抽取3件,求抽到的3件产品中优等品数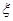 的分布列及数学期望。
的分布列及数学期望。
(本小题满分12分)已知等差数列 的前
的前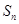 项和为
项和为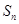 ,
,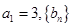 为等比数列,且
为等比数列,且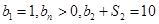 ,
,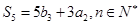 。
。
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)求数列 的前n项和
的前n项和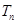 。
。
(本小题满分10分)在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,且
,且 。
。
(1)求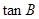 ;
;
(2)若 ,求
,求 的周长的最大值.
的周长的最大值.