给定椭圆 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是 .
.
(1)若椭圆C上一动点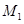 满足
满足 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为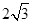 ,求P点的坐标;
,求P点的坐标;
(3)已知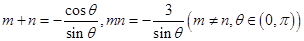 ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点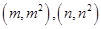 的直线的最短距离
的直线的最短距离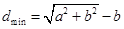 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
如图所示的几何体中,矩形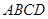 和矩形
和矩形 所在平面互相垂直,
所在平面互相垂直, 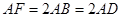 ,
,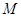 为
为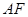 的中点,
的中点,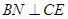 。
。
(Ⅰ)求证: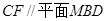 ;
;
(Ⅱ)求证: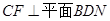 。
。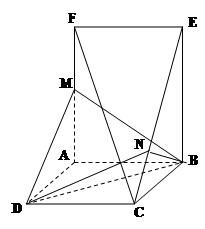
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组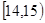 ……第五组
……第五组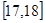 ,如图是按上述分组方法得到的频率分布直方图。
,如图是按上述分组方法得到的频率分布直方图。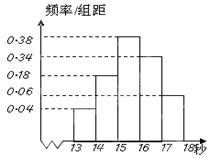
(Ⅰ) 在第一组和第五组内任取两个学生,记这两人的百米测试成绩分别为 求事件“
求事件“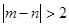 ”的概率;
”的概率;
(Ⅱ) 根据有关规定,成绩小于16秒为达标.如果男女生使用相同的达标
标准,则男女生达标情况如附表:
| 性别 是否达标 |
男 |
女 |
合计 |
| 达标 |
 |
 ___ ___ |
_____ |
| 不达标 |
 ___ ___ |
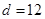 |
_____ |
| 合计 |
______ |
______ |
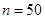 |
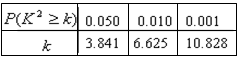
完成上述2×2列联表,根据上表数据,能否有99%的把握认为“体育达标与性别有关”?若有,你能否 提出一个更好的解决方法来?
提出一个更好的解决方法来?
附:
已知等差数列{ }满足
}满足 ,
, 。
。
(I)求数列{ }的通项公式;
}的通项公式;
(II)记 ,求数列
,求数列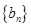 的前n项和
的前n项和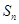 。
。
设 ,
, 分别是椭圆E:
分别是椭圆E: +
+ =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过 的直线
的直线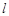 与E相交于A、B两点,且
与E相交于A、B两点,且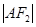 ,
,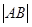 ,
,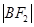 成等差数列。
成等差数列。
(Ⅰ)求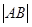
(Ⅱ)若直线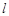 的斜率为1,求b的值。
的斜率为1,求b的值。
已知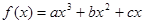 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间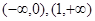 上是减函数,又
上是减函数,又
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.