某校从高三年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高三年级共有学生640名,试估计该校高三年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
已知二次函数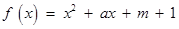 ,及函数
,及函数 。
。
关于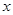 的不等式
的不等式 的解集为
的解集为 ,其中
,其中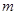 为正常数。
为正常数。
(1)求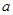 的值;
的值;
(2)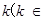 R
R 如何取值时,函数
如何取值时,函数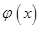
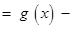
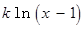 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若 ,且
,且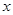
 ,求证:
,求证:
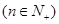 。
。
已知函数 ,
,
(1)若x=1时 取得极值,求实数
取得极值,求实数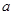 的值;
的值;
(2)当 时,求
时,求 在
在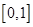 上的最小值;
上的最小值;
(3)若对任意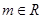 ,直线
,直线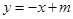 都不是曲线
都不是曲线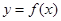 的切线,求实数
的切线,求实数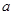 的取值范围。
的取值范围。
已知函数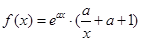 ,其中
,其中 ,
, .
.
(1)当 时,求曲线
时,求曲线 在点
在点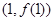 处的切线方程;
处的切线方程;
(2)求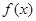 的单调区间.(要写推理过程)
的单调区间.(要写推理过程)
设函数 对任意实数x 、y都有
对任意实数x 、y都有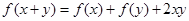 ,
,
(1)求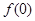 的值;
的值;
(2)若 ,求
,求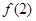 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想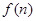
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
已知二项式
(1)当n=4时,写出该二项式的展开式;
(2)若展开式的前三项的二项式系数的和等于79,则展开式中第几项的二项式系数最大?