已知 展开式的二项式系数之和为256.
展开式的二项式系数之和为256.
(1)求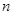 ;
;
(2)若展开式中常数项为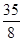 ,求
,求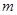 的值;
的值;
(3)若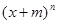 展开式中系数最大项只有第6项和第7项,求
展开式中系数最大项只有第6项和第7项,求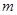 的取值情况.
的取值情况.
(本小题满分13分) 已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为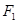 和
和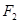 ,且|
,且|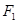
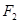 |=2,点(1,
|=2,点(1,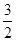 )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过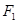 的直线
的直线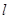 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若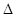 A
A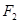 B的面积为
B的面积为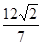 ,求以
,求以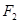 为圆心且与直线
为圆心且与直线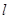 相切圆的方程.
相切圆的方程.
(本小题满分12分) 如图,在四棱锥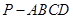 中,
中, ,
,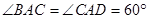 ,
, 平面
平面 ,
,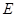 为
为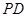 的中点,
的中点,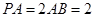 .
.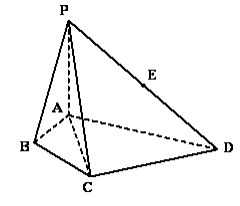
(1)求证: ∥平面
∥平面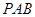 ;
;
(2)求四面体 的体积.
的体积.
(本小题满分12分) 已知函数 ,
,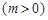 的最大值为2.
的最大值为2.
(1)求函数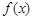 在
在 上的值域;
上的值域;
(2)已知 外接圆半径
外接圆半径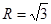 ,
,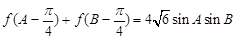 ,角
,角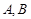 所对的边分别是
所对的边分别是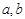 ,求
,求 的值.
的值.
(本小题满分12分)已知幂函数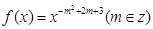 为偶函数,且在区间
为偶函数,且在区间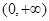 上是单调增函数
上是单调增函数
(1)求函数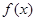 的解析式;
的解析式;
(2)设函数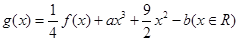 ,其中
,其中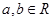 .若函数
.若函数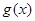 仅在
仅在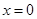 处有极值,求
处有极值,求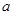 的取值范围.
的取值范围.
已知函数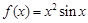 ,各项均不相等的有限项数列
,各项均不相等的有限项数列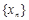 的各项
的各项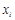 满足
满足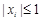 .令
.令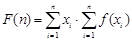 ,
,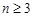 且
且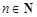 ,例如:
,例如: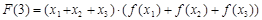 .
.
(Ⅰ)若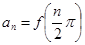 ,数列
,数列 的前n项和为Sn,求S19的值;
的前n项和为Sn,求S19的值;
(Ⅱ)试判断下列给出的三个命题的真假,并说明理由。
①存在数列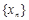 使得
使得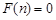 ;②如果数列
;②如果数列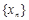 是等差数列,则
是等差数列,则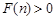 ;
;
③如果数列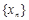 是等比数列,则
是等比数列,则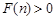 。
。