设圆C与两圆(x+ )2+y2=4,(x-
)2+y2=4,(x- )2+y2=4中的一个内切,另一个外切.
)2+y2=4中的一个内切,另一个外切.
(1)求C的圆心轨迹L的方程;
(2)已知点M(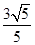 ,
,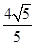 ),F(
),F( ,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.
,0),且P为L上动点,求||MP|-|FP||的最大值及此时点P的坐标.
在直三棱柱ABC—A1B1C1中, ,P为A1C1的中点,AB=BC=kPA。
,P为A1C1的中点,AB=BC=kPA。
(I)求三棱锥P—AB1C与三棱锥C1—AB1P的体积之比;
(II) 当k为何值时,直线PA
当k为何值时,直线PA
(本小题满分12分)某人上楼梯,每步上一阶的概率为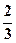 ,每步上二阶的概率为
,每步上二阶的概率为 ,设该人从台阶下的平台开始出发,到达第n阶的概率为
,设该人从台阶下的平台开始出发,到达第n阶的概率为 。
。
(Ⅰ)求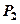 ;(Ⅱ)该人共走了5步,求
;(Ⅱ)该人共走了5步,求 该人这5步共上的阶数ξ的数学期望。
该人这5步共上的阶数ξ的数学期望。
(本小题满分10分)若函数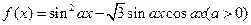 的图象与直线
的图象与直线 相切,相邻切点之间的距离为
相切,相邻切点之间的距离为 。
。
(Ⅰ)求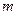 和
和 的值;
的值;
(Ⅱ)若点 是
是 图象的对称中心,且
图象的对称中心,且 ,求点
,求点 的坐标。
的坐标。
实验班学生必答题设数列 和
和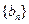 满足:
满足: ,且数列
,且数列 (
( )是等差数列,
)是等差数列, 对
对 恒成立
恒成立
(1)求数列 和
和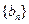 的通项公式;
的通项公式;
(2)是否存在 ,使
,使 ?若存在,求出
?若存在,求出 ,若不存在,说明理由。
,若不存在,说明理由。
已知数列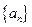 前n项和为
前n项和为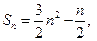 数列
数列 满足
满足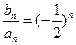 对任意正整数n都成立,
对任意正整数n都成立,
(1)求数列 的通项公式
的通项公式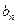 与前n项和Tn的表达式;
与前n项和Tn的表达式;
(2)若 对
对 恒成立,求k的最小值。
恒成立,求k的最小值。