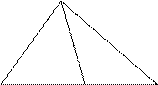
椭圆C的中心在原点,焦点在x轴上,两焦点F1,F2之间的距离为2 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
(10分)
在等差数列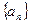 中,
中, 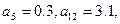 求
求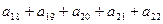
 的值
的值
.已知数列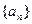 满足:
满足: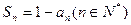 ,其中
,其中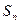 为数列
为数列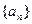 的前
的前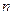 项和.(Ⅰ)试求
项和.(Ⅰ)试求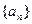 的通项公式;(
的通项公式;( Ⅱ)若数列
Ⅱ)若数列 满足:
满足: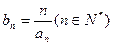 ,试求
,试求 的前
的前 项和公式
项和公式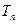 ;(III)设
;(III)设 ,数列
,数列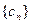 的前
的前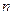 项和为
项和为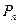 ,求证:
,求证: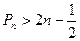 .
.
已知数列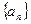 的前
的前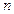 项和为
项和为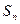 ,对任意
,对任意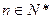 ,点
,点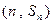 都在函数
都在函数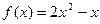 的图像上.
的图像上.
(1)求数列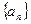 的通项公式;
的通项公式;
(2)设 ,
,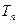 是数列
是数列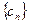 的前
的前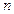 项和,求使得
项和,求使得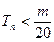 对所有
对所有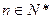 都成立的最小正整数
都成立的最小正整数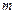 .
.
、已知向量 与
与 共线,其中
共线,其中 是
是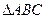 的内角,(1)求角
的内角,(1)求角 的大小;
的大小;
(2)若 ,求
,求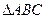 的面积S的最大值,并判断S取得最大值时
的面积S的最大值,并判断S取得最大值时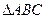 的形状.
的形状.
港口 北偏东
北偏东 方向的
方向的 处有一检查站,港口正东方向的
处有一检查站,港口正东方向的 处有一轮船,距离检查站为31海里,该轮船从
处有一轮船,距离检查站为31海里,该轮船从 处沿正西方向航行20海里后到达
处沿正西方向航行20海里后到达 处观测站,已知观测站与检查站距离21海里,问此时轮船离港口
处观测站,已知观测站与检查站距离21海里,问此时轮船离港口 还有多远?
还有多远?
|
|
|
|