有六名同学报名参加三个智力竞赛项目,在下列情况下各有多少种不同的报名方法?(不一定六名同学都能参加)
(1)每人恰好参加一项,每项人数不限;
(2)每项限报一人,且每人至多参加一项;
(3)每项限报一人,但每人参加的项目不限.
(本小题满分12分)已知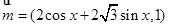 ,
, ,满足
,满足 =0
=0
(1)将y表示为x的函数f(x),并求f(x)的最小正周期;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f(x)≤f( )对所有x∈R恒成立,且a=2,求b+c的取值范围.
)对所有x∈R恒成立,且a=2,求b+c的取值范围.
(本小题满分10分)选修4-5:不等式选讲:
已知函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数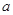 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程:
以直角坐标系的原点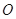 为极点,
为极点,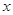 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为 (
(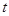 为参数,
为参数,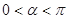 ),曲线
),曲线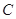 的极坐标方程为
的极坐标方程为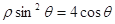 .
.
(Ⅰ)求曲线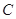 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线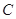 相交于
相交于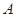 、
、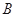 两点,当
两点,当 变化时,求
变化时,求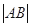 的最小值.
的最小值.
(本小题满分10分)选修4-1:几何证明选讲:
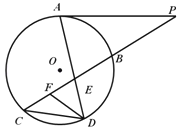
如图所示,已知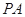 与⊙
与⊙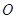 相切,
相切,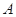 为切点,过点
为切点,过点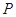 的割线交圆于
的割线交圆于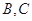 两点,弦
两点,弦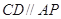 ,
,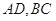 相交于点
相交于点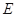 ,
,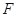 为
为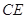 上一点,且
上一点,且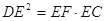 .
.
(Ⅰ)求证: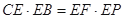 ;
;
(Ⅱ)若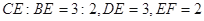 ,求
,求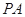 的长.
的长.
已知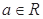 ,函数
,函数
(Ⅰ)若 ,求曲线
,求曲线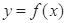 在点
在点 处的切线方程.
处的切线方程.
(Ⅱ)若 ,求
,求 在闭区间
在闭区间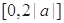 上的最小值.
上的最小值.