已知(
－
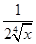)n的展开式中，前三项系数的绝对值依次成等差数列．
(1)证明：展开式中没有常数项；
(2)求展开式中所有的有理项．
（本小题满分12分）已知数列
的前
项和为
，且有
．
（1）求数列
的通项公式；
（2）若
求数列
的前n项和
设
的内角
所对的边分别为
且
．
（1）求角
的大小;
（2）若
,求的周长的取值范围．
已知函数
（
），
（1）求函数
的最小值；
（2）已知
，
：关于
的不等式
对任意恒成立；
：函数
是增函数．若“或”为真，“且”为假，求实数
的取值范围．
已知函数
，
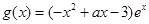（a为实数）．
（1）当a=5时，求函数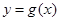
在
处的切线方程；
（2）求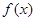
在区间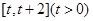
上的最小值；
（3）若存在两不等实数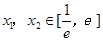
，使方程
成立，求实数a的取值范围．
为改善购物环境，提高经济效益，某商场决定投资800万元改造商场内部环境，据调查，改造好购物环境后，任何一个月内（每月按30天计算）每天的顾客人数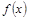
与第x天近似地满足
（千人），且每位顾客人均购物金额数
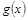近似地满足
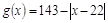（元）．
（1）求该商场第x天的销售收入
（单位千元，1≤x≤30，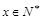
）的函数关系；
（2）若以最低日收入的20％作为每一天纯收入的计量依据，商场决定以每日纯收入的5％收回投资成本，试问商场在两年内能否收回全部投资成本.