某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次 购物量 |
1至 4件 |
5至 8件 |
9至 12件 |
13至 16件 |
17件及 以上 |
| 顾客数(人) |
x |
30 |
25 |
y |
10 |
| 结算时间 (分钟/人) |
1 |
1.5 |
2 |
2.5 |
3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值;
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
已知函数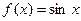 ,
,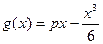
(I) 在(I)的条件下,求证:当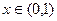 时,
时,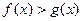 恒成立
恒成立
(II) 若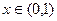 时
时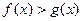 恒成立,求
恒成立,求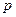 的取值范围
的取值范围
有一个3×3×3的正方体, 它的六个面上均涂上颜色. 现将这个长方体锯成27个1×1×1的小正方体,从这些小正方体中随机地任取1个.
如每次从中任取一个小正方体,确定涂色的面数后,再放回,连续抽取6次,设恰好取到只有一个面涂有颜色的小正方体的次数为 . 求
. 求 的数学期望.
的数学期望.
已知函数
(I)设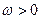 为常数,若
为常数,若 上是增函数,求
上是增函数,求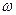 的取值范围
的取值范围
(II)若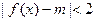 成立的充分条件是
成立的充分条件是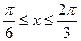 ,求实数m的取值范围
,求实数m的取值范围
(1)求实数 的值;
的值;
(2)求函数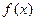 的图象与
的图象与 轴公共点的个数;
轴公共点的个数;
(3) ,使
,使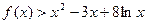 成立,求实数
成立,求实数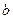 的取值范围.(参考数据:
的取值范围.(参考数据: ,
, )
)
(1)若离心率为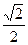 ,求椭圆的方程;
,求椭圆的方程;
(2)当
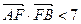 时,求椭圆离心率的取值范围
时,求椭圆离心率的取值范围