证明:已知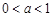 ,则
,则
现有甲乙两个团队之间进行某种比赛,与身高有很大的关系(假定忽略其它因素),为了预知比赛结果,在甲乙两个团队中各随机抽调出8人,测量身高并绘出茎叶图如图。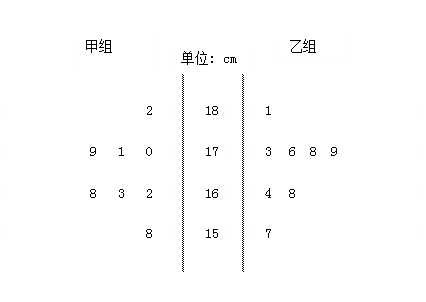
(1)请你根据茎叶图判断一下如果是跨越障碍物比赛,哪个团队胜出的可能性大一些?说明你的理由。
(2)如果是进行队形整齐性比赛(身高相对要整齐),哪个团队胜出的可能性又大一些?说明你的理由。
(3)从甲团队的这抽出的8人中的身高低于170cm的队员中再抽取两名进行某种灵巧性训练,则身高为158cm的那位队员被选中的概率是多少?
已知函数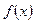 为定义在R上的奇函数,且当
为定义在R上的奇函数,且当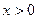 时,
时,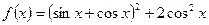 ,
,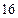
(1)求 时
时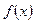 的表达式;
的表达式;
(2)若关于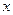 的方程
的方程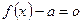 有解,求实数
有解,求实数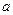 的范围。
的范围。
.以连续抛掷两枚骰子先后得到的点数m,n为P点的坐标(m,n)时,
(1)用列举法写出点P(m,n)的所有结果;
(2)若点P落在直线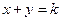 (
(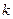 为常数)上且使此事件的概率最大,求
为常数)上且使此事件的概率最大,求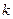 的值;
的值;
(3)求P点落在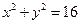 内部的概率.
内部的概率.
求.函数y=2sin(x
 )取得最大值与最小值的自变量集合,并写出最大、最小值及单调减区间
)取得最大值与最小值的自变量集合,并写出最大、最小值及单调减区间
.求函数 的定义域
的定义域