已知 ,试证明
,试证明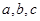 至少有一个不小于1.
至少有一个不小于1.
某班50名学生在一次百米 测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组
测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组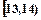 ;第二组
;第二组 ……第五组
……第五组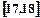 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图. 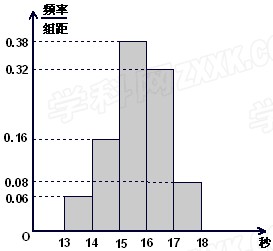
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设 、
、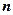 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知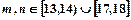 .求事件“
.求事件“ ”的概率.
”的概率.
设函数
(Ⅰ)求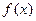 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若关于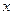 的方程
的方程 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
某商场举行抽奖活动,从装有编号0,1,2,3四个小球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖, 等于3中三等奖.
等于3中三等奖.
(Ⅰ)求中三等奖的概率; (Ⅱ)求中奖的概率.
(Ⅱ)求中奖的概率.
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘 法求出y关于x的线性回归方程y=
法求出y关于x的线性回归方程y=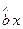 +
+ ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程 预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(参考公式:回归直线的方程是 ,其中
,其中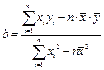 ,
, ,)
,)
某高校 “ 统计初步 ” 课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
| 性别专业 |
非统计专业 |
统计专业 |
| 男 |
13 |
10 |
| 女 |
7 |
20 |
列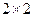 列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。
列联表,利用独立性检验的方法,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系。