解下列不等式:
(1)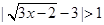 (2)
(2)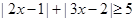
已知函数 .
.
(1)当 时,解不等式
时,解不等式 ;
;
(2)若 时,
时, ,求a的取值范围.
,求a的取值范围.
长为3的线段两端点A,B分别在x轴正半轴和y轴的正半轴上滑动, ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.
(1)以直线AB的倾斜角 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;
(2)求点P到点 距离的最大值.
距离的最大值.
如图,E是圆O内两弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.
求证:(1) ;(2)EF//CB.
;(2)EF//CB.
已知函数 ,
, .
.
(1)若存在 ,使得
,使得 ,求a的取值范围;
,求a的取值范围;
(2)若 有两个不同的实数解
有两个不同的实数解 ,证明:
,证明: .
.
已知抛物线 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆 的两条切线,切点为A、B,
的两条切线,切点为A、B, .
.
(1)求抛物线E的方程;
(2)过抛物线E上的点N作圆C的两条切线,切点分别为P、Q,若P,Q,O(O为原点)三点共线,求点N的坐标.