某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响．已知某学生只选修甲的概率为0．08，只选修甲和乙的概率是0．12，至少选修一门的概率是0．88，用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积．
(1)记“函数f(x)＝x2＋ξx为R上的偶函数”为事件A，求事件A的概率；
(2)求ξ的分布列．
A、B、C、D、E五人分四本不同的书，每人至多分一本，求：
(1)A不分甲书，B不分乙书的概率；
(2)甲书不分给A、B，乙书不分给C的概率。
从分别写有0，1，2，3，4，5，6的七张卡片中，任取4张，组成没有重复数字的四位数，计算：
(1)这个四位数是偶数的概率；
(2)这个四位数能被9整除的概率；
(3)这个四位数比4510大的概率。
某班数学兴趣小组有男生和女生各３名，现从中任选２名学生去参加校数学竞赛，求
（I） 恰有一名参赛学生是男生的概率；
（II）至少有一名参赛学生是男生的概率；
（Ⅲ）至多有一名参赛学生是男生的概率。
掷两枚骰子，求所得的点数之和为6的概率．
设f(x)=x3+3x2+px, g(x)=x3+qx2+r，且y=f(x)与y=g(x)的图象关于点（0，1）对称．（1）求p、q、r的值；（2）若函数g(x)在区间(0，m)上递减，求m的取值范围；（3）若函数g(x)在区间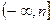
上的最大值为2，求n的取值范围．