某工厂生产A，B两种元件，其质量按测试指标划分，指标大于或等于82为正品，小于82为次品．现随机抽取这两种元件各100个进行检测，检测结果统计如下：
| 测试 指标 |
[70,76) |
[76,82) |
[82,88) |
[88,94) |
[94,100] |
| 元件A |
8 |
12 |
40 |
32 |
8 |
| 元件B |
7 |
18 |
40 |
29 |
6 |
(1)试分别估计元件A，元件B为正品的概率；
(2)生产1个元件A，若是正品则盈利40元，若是次品则亏损5元；生产1个元件B，若是正品则盈利50元，若是次品则亏损10元．在(1)的前提下，
(ⅰ)X为生产1个元件A和1个元件B所得的总利润，求随机变量X的分布列和数学期望；
(ⅱ)求生产5个元件B所得利润不少于140元的概率．
已知函数f(x)=
在点(-1,f(-1))处的切线方程为x+y+3=0.
(1)求函数f(x)的解析式.
(2)设g(x)=lnx.求证:g(x)≥f(x)在[1,+∞)上恒成立.
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①试从上述五个式子中选择一个,求出这个常数.
②根据①的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数.
某少数民族的刺绣有着悠久的历史,如图(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.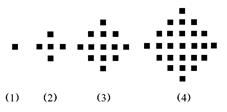
(1)求出f(5).
(2)利用合情推理的“归纳推理思想”归纳出f(n+1)与f(n)的关系式,并根据你得到的关系式求f(n)的关系式.
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)