对于三次函数 ,定义
,定义 是
是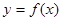 的导函数
的导函数 的导函数,若方程
的导函数,若方程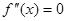 有实数解
有实数解 ,则称点
,则称点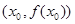 为函数
为函数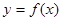 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数 都关于点
都关于点 对称:
对称:
②存在三次函数 ,若
,若 有实数解
有实数解 ,则点
,则点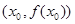 为函数
为函数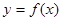 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 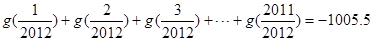
其中所有正确结论的序号是( ).
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |
如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.
(1)求直角三角形的三边长;
(2)求两直角边在斜边上的射影的长.
如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=10,BD=8,求CD的长.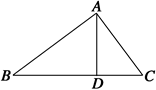
如图所示,AD、CE是△ABC中边BC、AB的高,AD和CE相交于点F.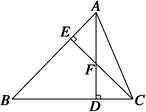
求证:AF·FD=CF·FE.
(拓展深化)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α.且DM交AC于F,ME交BC于G,
(1)写出图中三对相似三角形,并证明其中的一对;
(2)连接FG,如果α=45°,AB=4 ,AF=3,求FG的长.
,AF=3,求FG的长.
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.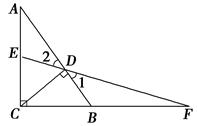
求证:FD2=FB·FC.