设函数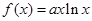
，已知曲线
在点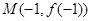
处的切线方程是
．
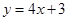（1）求
的值；并求出函数的单调区间；
（2）求函数
在区间
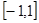上的最值．
（本小题满分10分）选修4-5：不等式选讲
（Ⅰ）求证：已知
都是正实数，求证：
；
（Ⅱ）求证：已知
都是正数，求证：
.
（本小题满分10分）选修4-4：坐标系与参数方程
已知曲线
：
（
为参数），
：
（
为参数）.
（Ⅰ）化、的方程为普通方程，并说明它们分别表示什么曲线；
（Ⅱ）若曲线上的点
对应的参数为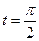
，
为曲线上的动点，求线段
中点
到直线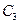
：
（为参数）距离的最
小值.
（本小题满分10分）选修4-1：几何证明选讲
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连结EC、CD.
（Ⅰ）求证：直线AB是⊙O的切线；
（Ⅱ）若tan∠CED=
，⊙O的半径为3，求OA的长.
.(本小题满分12分）
已知二次函数
对
都满足
且
，设函数
（
，
）．
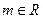（Ⅰ）求的表达式；
（Ⅱ）若
，使
成立，求实数
的取值范围；
（Ⅲ）设
，
，求证：对于
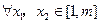，恒有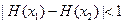
.
(本小题满分12分）
某公园的大型中心花园的边界为椭圆，花园内种植各种花草. 为增强观赏性，在椭圆内以其
中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草（如图），并以该直角三角
形斜边开辟观赏小道（其中的一条为线段
）. 某园林公司承接了该中心花园的施工建设，
在施工时发现，椭圆边界上任意一点到椭圆两焦点的距离和为4（单位：百米），且椭圆上点
到焦点的最近距离为1（单位：百米）.
（Ⅰ）以椭圆中心为原点建立如图的坐标系，求该椭圆的标准方程；
（Ⅱ）请计算观赏小道的长度（不计小道宽度）的最大值.
 |