某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
| X |
1 |
2 |
3 |
4 |
| Y |
51 |
48 |
45 |
42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
已知椭圆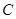 的中心为直角坐标系
的中心为直角坐标系 的原点,焦点在
的原点,焦点在 轴上,它的一个顶点到两个焦点的距离分别是7和1.
轴上,它的一个顶点到两个焦点的距离分别是7和1.
(1)求椭圆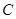 的方程;
的方程;
(2)若 为椭圆
为椭圆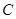 的动点,
的动点, 为过
为过 且垂直于
且垂直于 轴的直线上的点,
轴的直线上的点,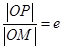 (
(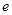 为椭圆的离心率),求点
为椭圆的离心率),求点 的轨迹方程,并说明轨迹是什么曲线.
的轨迹方程,并说明轨迹是什么曲线.
已知双曲线 ,
, 、
、 是双曲线的左右顶点,
是双曲线的左右顶点, 是双曲线上除两顶点外的一点,直线
是双曲线上除两顶点外的一点,直线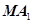 与直线
与直线 的斜率之积是
的斜率之积是 ,
,
求双曲线的离心率;
若该双曲线的焦点到渐近线的距离是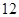 ,求双曲线的方程.
,求双曲线的方程.
如图,抛物线关于 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2),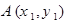 ,
, 均在抛物线上.
均在抛物线上.
(1)求该抛物线方程;
(2)若AB的中点坐标为 ,求直线AB方程.
,求直线AB方程.
已知函数 ,
, .
.
(1)如果函数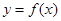 在
在 上是单调减函数,求
上是单调减函数,求 的取值范围;
的取值范围;
(2)是否存在实数 ,使得方程
,使得方程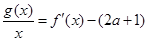 在区间
在区间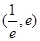 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数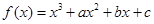 在
在 与
与 时,都取得极值.
时,都取得极值.
(1)求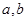 的值;
的值;
(2)若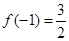 ,求
,求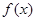 的单调区间和极值;
的单调区间和极值;
(3)若对 都有
都有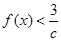 恒成立,求
恒成立,求 的取值范围.
的取值范围.