如图，正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上，连接BF、DF.
（1）求证：BF=DF；
（2）连接CF，请直接写出BE∶CF的值（不必写出计算过程）.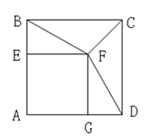
求下列二次函数的图像与x轴的交点坐标,并作草图验证.
(1)y=
x2+x+1; (2)y="4x2-8x+4;" (3)y="-3x2-6x-3;" 
(4)y=-3x2-x+4
如图，A、B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°方向，在B城的北偏西45°方向，且C城与A城相距120千米，B城在A城的正东方向，以C为圆心，以60千米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市间修建一条笔直的高速公路，（14＇）
（1）请你计算公路的长度。（结果保留根号）
（2）请你分析这条公路有没有可能是对古迹或文物赞成损毁。
如图，小明在楼上点A处观察旗杆BC，测得旗杆顶部B的仰角为30°，测得旗杆底部C的俯角为60°，已知点A距地面高AD为12m，求旗杆的高度。（12＇）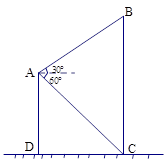
如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE，
（1）求证：△ABE≌△DFA。
（2）如果AD＝10，AB＝6，求sin∠EDF的值。
如图，在Rt△ABC中，∠C=90°，CD⊥AB于D，已知sinA=
，BD=2，求BC的长。