设全集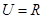 ,
,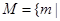 关于
关于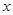 的方程
的方程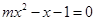 有实数根},
有实数根}, 关于
关于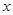 的方程
的方程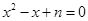 有实数根},
有实数根},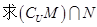 .
.
(本小题满分12分)已知二次函数 (
(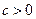 )的导函数的图象如图所示:
)的导函数的图象如图所示:
(Ⅰ)求函数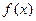 的解析式;
的解析式;
(Ⅱ)令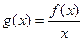 ,求
,求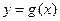 在
在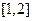 上的最大值.
上的最大值.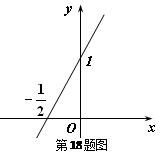
(本小题满分12分)在锐角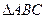 中 ,三个内角A、B、C的对边分别为a、b、c,且满足
中 ,三个内角A、B、C的对边分别为a、b、c,且满足
(1)求 的值;
的值;
(2)若b=3,求a+c的最大值。
(本小题满分12分)已知锐角三角形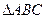 内角A、B、C对应边分别为a,b,c。
内角A、B、C对应边分别为a,b,c。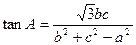
(Ⅰ)求A的大小;(Ⅱ)求 的取值范围。
的取值范围。
(本小题满分12分)已知二次函数f(x)=ax2+bx+c和一次函数g(x)=-bx,其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证:函数 图象交于不同的两点;
图象交于不同的两点;
(2)设(1)问中交点为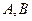 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。
(选修4—5:不等式选讲)设函数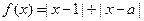
(1)若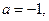 解不等式
解不等式 ;
;
(2)如果 ,
,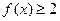 ,求
,求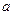 的取值范围。
的取值范围。