已知:0<a<b<c<d 且a+d=b+c,求证: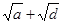 <
< 
求下列定积分
(1)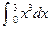 (2)
(2)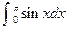 (3)
(3)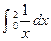
求由抛物线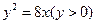 与直线
与直线 及
及 所围成图形的面积.
所围成图形的面积.
一物体按规律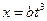 做直线运动,式中
做直线运动,式中 为时间t内通过的距离,媒质的阻力与速度的平方成正比(比例常数为
为时间t内通过的距离,媒质的阻力与速度的平方成正比(比例常数为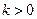 ),试求物体由
),试求物体由 运动到
运动到 时,阻力所做的功.
时,阻力所做的功.
今有一块边长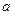 的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,
的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大, 值应为多少?
值应为多少?
设某物体一天中的温度T是时间t的函数,已知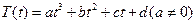 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?