过曲线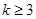 :
: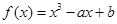 外的点
外的点 作曲线
作曲线 的切线恰有两条,
的切线恰有两条,
(1)求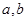 满足的等量关系;
满足的等量关系;
(2)若存在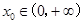 ,使
,使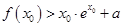 成立,求
成立,求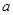 的取值范围.
的取值范围.
设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0,x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,1]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(I)证明:对任意的 ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f( ),则(0,
),则(0, )为含峰区间:若f(
)为含峰区间:若f( )
) f(
f( ),则
),则 为含峰区间:
为含峰区间:
(II)对给定的r(0<r<0.5),证明:存在 ∈(0,1),满足
∈(0,1),满足 ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r:
(III)选取 ∈(O,1),,由(I)可确定含峰区间为
∈(O,1),,由(I)可确定含峰区间为 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 与
与 或
或 与
与 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, )的情况下,试确定的值
)的情况下,试确定的值 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
已知数列 满足:
满足:
(1)若 ,求数列
,求数列 的前30项和
的前30项和 的值;
的值;
(2)求证:对任意的实数a,总存在正整数m,使得当n>m( )时,
)时,  成立。
成立。
某产品按质最分成6种不同档次。假设工时不变,每天可生产最低档次40件。若每提高一个档次,每件利润增加1元,但是每天要少生产2件产品。
(1)若最低档次产品利润每件为16元时,问生产哪种档次产品每天所获利润最大?
(2)由于原材料价格的浮动,生产最低档次产品每什利润a [8,24]元,那么生产哪种档次产品利润最大?
[8,24]元,那么生产哪种档次产品利润最大?
已知:以点 为圆心的圆与x轴交于点O,A,与Y轴交于点O,B,其中O为原点.
为圆心的圆与x轴交于点O,A,与Y轴交于点O,B,其中O为原点.
(1)求证:△OAB的面积为定值:
(2)设直线y=-2x+4与圆C交于点M,N,若OM= ON,求圆C的方程.
.已知矩形 中,
中, ,
, 为
为 的中点,沿
的中点,沿 将
将 折起,使
折起,使 ,
, 分别为
分别为 的中点。
的中点。
(1)求证:直线
(2)求证:面