已知椭圆 过点
过点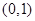 且离心率为
且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)若斜率为 的直线
的直线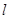 交
交 于
于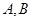 两点,且
两点,且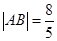 ,求直线
,求直线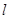 的方程.
的方程.
给定椭圆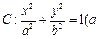 >
>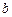 >0
>0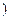 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为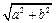 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆 的一个焦点为
的一个焦点为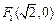 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;
(2)若倾斜角为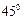 的直线
的直线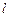 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆 的伴随圆相交于M、N两
的伴随圆相交于M、N两
点,求弦MN的长;
(3)点 是椭圆
是椭圆 的伴随圆上的一个动点,过点
的伴随圆上的一个动点,过点 作直线
作直线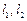 ,使得
,使得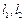 与椭圆
与椭圆 都只有一个公共点,求证:
都只有一个公共点,求证: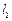 ⊥
⊥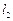 .
.
如图,α⊥β,α∩β=l, A∈α, B∈β,点A在直线l上的射影为A1, 点B在l的射影为B1,已知AB=2,AA1=1, BB1=, 求:
(Ⅰ) 直线AB分别与平面α,β所成角的大小;
(Ⅱ)二面角A1-AB-B1的余弦值.
(本小题满分12分)甲有一个装有 个红球、
个红球、 个黑球的箱子,乙有一个装有
个黑球的箱子,乙有一个装有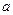 个红球、
个红球、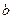 个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(
个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(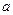 ,
,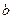 ,
, ,
,
 ).
).
(Ⅰ)当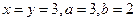 ,时,求甲获胜的概率;
,时,求甲获胜的概率;
(Ⅱ)当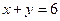 ,
,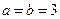 时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的
时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的 ,
, 值;
值;
(Ⅲ)当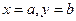 时,这个游戏规则公平吗?请说明理由.
时,这个游戏规则公平吗?请说明理由.
(本小题满分12分) 已知向量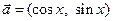 ,
, ,
, .
.
(1)若 求向量
求向量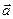 ,
,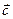 的夹角;
的夹角;
(2)当 时,求函数
时,求函数 的最大值。
的最大值。
(本小题满分14分)已知函数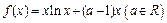 .
.
(Ⅰ)当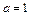 时,求曲线
时,求曲线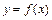 在
在 处的切线方程;
处的切线方程;
(Ⅱ)求函数 在区间
在区间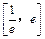 上的最小值;
上的最小值;
(Ⅲ)若关于的方程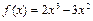 在区间
在区间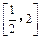 内有两个不相等的实数根,求实数a的取值范围.
内有两个不相等的实数根,求实数a的取值范围.