如图,在四棱锥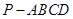 中,底面
中,底面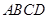 是矩形,
是矩形, 平面
平面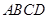 ,
,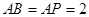 ,
, ,
, 依次是
依次是 的中点.
的中点.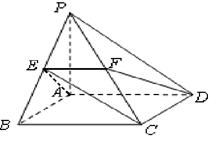
(1)求证: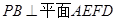 ;
;
(2)求直线 与平面
与平面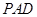 所成角的正弦值.
所成角的正弦值.
已知函数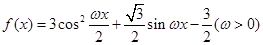 在一个周期内的图象如图所示,点
在一个周期内的图象如图所示,点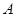 为图象的最高点,
为图象的最高点,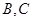 为图象与
为图象与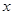 轴的交点,且三角形
轴的交点,且三角形 的面积为
的面积为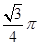 .
.
(Ⅰ)求 的值及函数
的值及函数 的值域;
的值域;
(Ⅱ)若 ,求
,求 的值.
的值.
命题 :不等式
:不等式 对一切实数
对一切实数 都成立;命题
都成立;命题 :已知函数
:已知函数 的图像在点
的图像在点 处的切线恰好与直线
处的切线恰好与直线 平行,且
平行,且 在
在 上单调递减。若命题
上单调递减。若命题 或
或 为真,求实数
为真,求实数 的取值范围。
的取值范围。
己知函数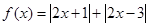 .
.
(I)若关于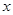 的不等式
的不等式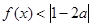 的解集不是空集,求实数
的解集不是空集,求实数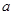 的取值范围;
的取值范围;
(II)若关于 的一元二次方程
的一元二次方程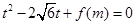 有实根,求实数
有实根,求实数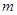 的取值范围.
的取值范围.
在直角坐标系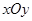 中,
中,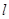 是过定点
是过定点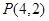 且倾斜角为
且倾斜角为 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点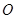 为极点,以
为极点,以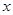 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线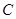 的极坐标方程为
的极坐标方程为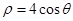 .
.
(I)写出直线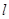 的参数方程;并将曲线
的参数方程;并将曲线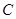 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(II)若曲线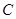 与直线相交于不同的两点
与直线相交于不同的两点 ,求
,求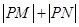 的取值范围.
的取值范围.
如图所示,己知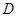 为
为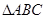 的
的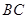 边上一点,
边上一点,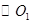 经过点
经过点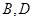 ,交
,交 于另一点
于另一点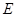 ,
, 经过点
经过点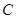 ,
,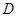 ,交
,交 于另一点
于另一点 ,
,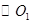 与
与 的另一交点为
的另一交点为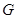 .
.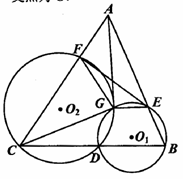
(I)求证: 四点共圆;
四点共圆;
(II)若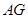 切
切 于
于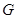 ,求证:
,求证: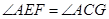 .
.