(本小题8分)已知数列 的前
的前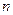 项和为
项和为 ,点
,点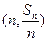 在直线
在直线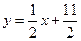 上;数列
上;数列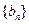 满足
满足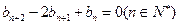 ,且
,且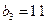 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列 、
、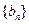 的通项公式;
的通项公式;
(2)设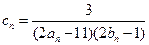 ,求数列
,求数列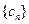 的前
的前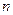 项和为
项和为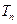 .
.
(本小题8分)已知函数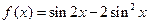
(1)求函数 的最小正周期.
的最小正周期.
(2)求函数 的最大值及
的最大值及 取最大值时x的集合.
取最大值时x的集合.
(本小题满分14分)已知{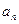 }(
}( 是正整数)是首项是
是正整数)是首项是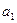 ,公比是
,公比是 的等比数列.
的等比数列.
(1)求和: ;
;
(2)由(1)的结果归纳概括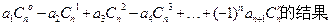
并加以证明;
(3)设 是等比数列的前
是等比数列的前 项的和,求
项的和,求
(本小题满分12分)如图所示,平面 平面
平面 ,
, 是等边三角形,
是等边三角形, 是矩形,
是矩形,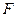 是
是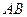 的中点,
的中点, 是
是 的中点,
的中点, 与平面
与平面 成
成 角.
角.
(1)求证: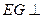 平面
平面 ;
;
(2)若 ,求二面角
,求二面角 的度数;
的度数;
(3)当 的长是多少时,
的长是多少时, 点到平面
点到平面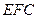 的距离为
的距离为 ?并说明理由
?并说明理由
甲、乙、丙三人组成一组,参加一个闯关游戏团体赛,三人各自独立闯关,其中甲闯关成功的概率为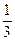 ,甲、乙都闯关成功的概率为
,甲、乙都闯关成功的概率为 ,乙、丙都闯关成功的概率为
,乙、丙都闯关成功的概率为 ,每人闯关成功得2分,三人得分之和记为小组团体总分.
,每人闯关成功得2分,三人得分之和记为小组团体总分.
(1)求乙、丙各自闯关成功的概率;
(2)求团体总分为4分的概率;
(3)若团体总分不小于4分,则小组可参加复赛,求该小组参加复赛的概率.