已知函数 ,
, .
.
(1)函数 的零点从小到大排列,记为数列
的零点从小到大排列,记为数列 ,求
,求 的前
的前 项和
项和 ;
;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)设点 是函数
是函数 与
与 图象的交点,若直线
图象的交点,若直线 同时与函数
同时与函数 ,
, 的图象相切于
的图象相切于 点,且
点,且
函数 ,
, 的图象位于直线
的图象位于直线 的两侧,则称直线
的两侧,则称直线 为函数
为函数 ,
, 的分切线.
的分切线.
探究:是否存在实数 ,使得函数
,使得函数 与
与 存在分切线?若存在,求出实数
存在分切线?若存在,求出实数 的值,并写出分切线方程;若不存在,请说明理由.
的值,并写出分切线方程;若不存在,请说明理由.
(8分)在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB和CD成60°角(见下图).求B、D间的距离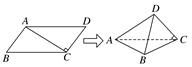
若f(x)=ax3+bx2,且f(x)在点P(-1,-2)处的切线恰好与直线3x-y=0垂直。(1)求a,b的值;(2)若f(x)在区间[0,m]上单调,求m的取值范围。
已知函数 。
。
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)若 在
在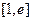 恒成立,求
恒成立,求 的取值范围。
的取值范围。
已知函数 ,
, ,其中
,其中 R.
R.
(Ⅰ)当a=1时判断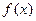 的单调性;
的单调性;
(Ⅱ)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数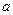 的取值范围;
的取值范围;
(Ⅲ)设函数 ,当
,当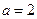 时,若
时,若 ,
, ,总有
,总有 成立,求实数
成立,求实数 的取值范围
的取值范围
已知函数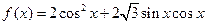
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)在 中,
中, 为内角
为内角 的对边,若
的对边,若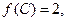
 ,求
,求 的最大面积。
的最大面积。