随机抽取某中学高一级学生的一次数学统测成绩得到一样本,其分组区间和频数是: ,2;
,2; ,7;
,7; ,10;
,10; ,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
,x;[90,100],2.其频率分布直方图受到破坏,可见部分如下图所示,据此解答如下问题.
(1)求样本的人数及x的值;
(2)估计样本的众数,并计算频率分布直方图中 的矩形的高;
的矩形的高;
(3)从成绩不低于80分的样本中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为 ,求
,求 的数学期望.
的数学期望.
(本小题满分14分)已知函数 (
( 是常数).
是常数).
(1)设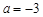 ,
, 、
、 是函数
是函数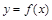 的极值点,试证明曲线
的极值点,试证明曲线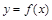 关于点
关于点 对称;
对称;
(2)是否存在常数 ,使得
,使得 ,
, 恒成立?若存在,求常数
恒成立?若存在,求常数 的值或取值范围;若不存在,请说明理由.
的值或取值范围;若不存在,请说明理由.
(注:,对于曲线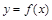 上任意一点
上任意一点 ,若点
,若点 关于
关于 的对称点为
的对称点为 ,则
,则 在曲线
在曲线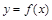 上.)
上.)
在平面直角坐标系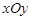 中,点A、B的坐标分别是
中,点A、B的坐标分别是 、
、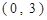 ,直线AM、BM相交于点M,且它们的斜率之积是
,直线AM、BM相交于点M,且它们的斜率之积是 .
.
(1)求点M的轨迹 方程;
方程;
(2)若直线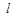 经过点
经过点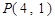 ,与轨迹
,与轨迹 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线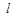 的方程.
的方程.
(本小题满分14分)已知在四棱锥 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
,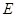 ,
,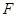 分别是线段
分别是线段 ,
, 的中点.
的中点.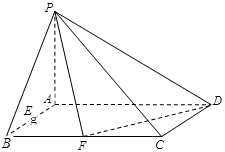
(1)判断并说明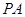 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出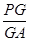 的值;若不
的值;若不
存在,请说明理由;
(2)若 与平面
与平面 所成的角为
所成的角为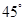 ,求二面角
,求二面角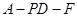 的平面角的余弦值.
的平面角的余弦值.
(本小题满分14分)已知 为等比数列,其中
为等比数列,其中 ,且
,且 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)近年来空气污染是一个生活中重要的话题, PM2.5就是其中一个指标。PM2.5指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.PM2.5日均值在35微克/立方米以下空气质量为一级:在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.淮北相山区2014年12月1日至I0日每天的PM2.5监测数据如茎叶图所示.
(1)期间的某天小刘来此地旅游,求当天PM2.5日均监测数据未超标的概率;
(2)陶先生在此期间也有两天经过此地,这两天此地PM2.5监测数据均未超标.请计算出这两天空气质量恰好有一天为一级的概率;
(3)从所给10天的数据中任意抽取三天数据,记 表示抽到PM2.5监测数据超标的天数,求
表示抽到PM2.5监测数据超标的天数,求 的分布列及期望.
的分布列及期望.