在平面直角坐标系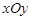 中,点A、B的坐标分别是
中,点A、B的坐标分别是 、
、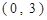 ,直线AM、BM相交于点M,且它们的斜率之积是
,直线AM、BM相交于点M,且它们的斜率之积是 .
.
(1)求点M的轨迹 方程;
方程;
(2)若直线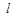 经过点
经过点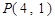 ,与轨迹
,与轨迹 有且仅有一个公共点,求直线
有且仅有一个公共点,求直线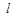 的方程.
的方程.
(本小题14分)已知函数 在
在 处取得极值。
处取得极值。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)求证:对于区间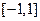 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
;
(Ⅲ)若过点 可作曲线
可作曲线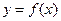 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。
(本小题满分12分)如图所示, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线 使
使 与
与 平行,若平行,求出直线
平行,若平行,求出直线 的方程, 若不平行,请说明理由.
的方程, 若不平行,请说明理由.
(本小题满分12分)如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)求线段PA上点Q的位置,使得PC//平面BDQ.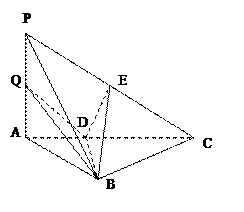
(本小题满分12分)已知函数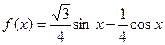 .
.
(Ⅰ)若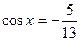 ,
,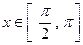 ,求函数
,求函数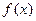 的值;
的值;
(Ⅱ)将函数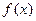 的图像向右平移
的图像向右平移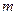 个单位,使平移后的图像关于原点对称,若
个单位,使平移后的图像关于原点对称,若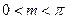 ,试求
,试求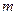 的值.
的值.
(本小题满分12分)青海玉树发生地震后,为重建,对某项工程进行竞标,现共有6家企业参与竞标,其中A企业来自辽宁省,B、C两家企业来自福建省,D、E、F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同。
(Ⅰ)列举所有企业的中标情况;
(Ⅱ)在中标的企业中,至少有一家来自福建省的概率是多少?