(本小题满分12分)如图所示, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线 使
使 与
与 平行,若平行,求出直线
平行,若平行,求出直线 的方程, 若不平行,请说明理由.
的方程, 若不平行,请说明理由.

(本小题满分10分)选修4—1,几何证明选讲
如图所示,圆 的两弦
的两弦 和
和 交于点
交于点 ,
, ∥
∥ ,
, 交
交 的延长线于点
的延长线于点 ,
, 切圆
切圆 于点
于点 .
.
(1)求证:△ ∽△
∽△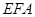 ;
;
(2)如果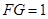 ,求
,求 的长.
的长.
(本小题满分12分)已知函数
(1)求函数 的单调区间;
的单调区间;
(2)当 时,
时, ,求实数
,求实数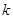 的取值范围
的取值范围
(本小题满分12分)已知椭圆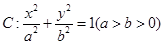 的离心率为
的离心率为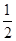 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线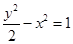 的焦点重合,过点
的焦点重合,过点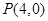 且不垂直于
且不垂直于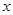 轴的直线
轴的直线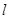 与椭圆
与椭圆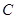 相交于
相交于 两点.
两点.
(1)求椭圆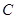 的方程;
的方程;
(2)求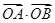 的取值范围.
的取值范围.
(本小题满分12分)如图,在斜三棱柱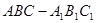 中,
中,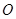 是
是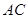 的中点,
的中点,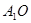 ⊥平面
⊥平面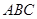 ,
, ,
,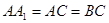 .
. 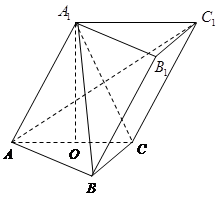
(1)求证: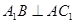 ;
;
(2)求二面角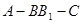 的余弦值.
的余弦值.
(本小题满分12分)某市规定,高中学生三年在校期间参加不少于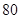 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段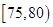 ,
,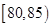 ,
, ,
, ,
,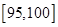 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记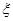 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量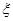 的分布列和数学期望
的分布列和数学期望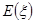 .
.