(本小题满分14分)已知在四棱锥 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
,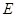 ,
,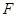 分别是线段
分别是线段 ,
, 的中点.
的中点.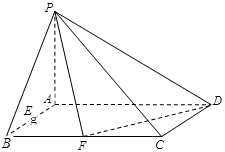
(1)判断并说明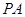 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,求出
?若存在,求出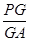 的值;若不
的值;若不
存在,请说明理由;
(2)若 与平面
与平面 所成的角为
所成的角为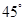 ,求二面角
,求二面角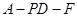 的平面角的余弦值.
的平面角的余弦值.
(本小题满分10分)选修4-5:不等式选讲
设函数
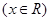 的最小值为a.
的最小值为a.
(1)求a;
(2)已知两个正数m,n满足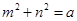 ,求
,求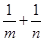 的最小值.
的最小值.
(本小题满分10分)选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系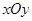 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同. 已知曲线C的极坐标方程为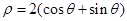 ,斜率为
,斜率为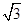 的直线
的直线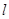 交y轴于点
交y轴于点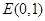 .
.
(1)求C的直角坐标方程,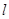 的参数方程;
的参数方程;
(2)直线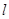 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求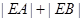 .
.
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形ABDC内接于圆,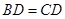 ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.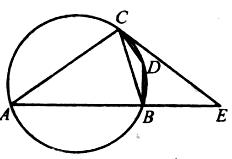
(1)求证: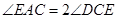 ;
;
(2)若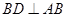 ,
,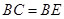 ,
,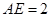 ,求AB的长.
,求AB的长.
(本小题满分12分)已知函数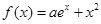 ,
,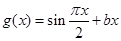 ,直线
,直线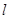 与曲线
与曲线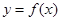 切于点
切于点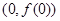 且与曲线
且与曲线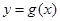 切于点
切于点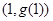 .
.
(1)求a,b的值和直线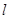 的方程;
的方程;
(2)证明: .
.
(本小题满分12分)已知抛物线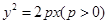 ,过点
,过点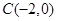 的直线
的直线 交抛物线于A,B两点,坐标原点为O,
交抛物线于A,B两点,坐标原点为O,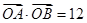 .
.
(1)求抛物线的方程;
(2)当以AB为直径的圆与y轴相切时,求直线 的方程.
的方程.