如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.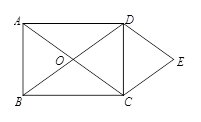
因式分解 :
(1)、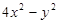 (2)、2a2-4ab+2b2
(2)、2a2-4ab+2b2
点A(-l,4)和点B(-5,1)在平面直角坐标系中的位置如图所示.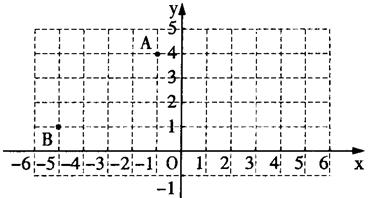
(1)将点A、B分别向右平移5个单位,得到点A1、B1,请画出四边形AA1B1B;
(2)画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线 过点A(—1,0),与⊙C相切于点D,求直线
过点A(—1,0),与⊙C相切于点D,求直线 的解析式。
的解析式。
已知 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 是切点,
是切点, 与⊙
与⊙ 交于点
交于点 .
.
(1)如图①,若 ,
, ,求
,求 的长(结果保留根号);
的长(结果保留根号);
(2)如图②,若 为
为 的中点,求证:直线
的中点,求证:直线 是⊙
是⊙ 的切线.
的切线.
在国家下达的宏观调控下,某市的商品房成交价由今年7月分的14000元/ 下降到9月份 的12600元/
下降到9月份 的12600元/ 。
。
⑴ 问8、9两月平均每月降价的百分率是多少?(参考数据: )
)
⑵ 如果房价继续回落,按此降价的百分率,你预测到11月分该市的商品房成交均价是否会
跌破10000元/ ?请说明理由。
?请说明理由。