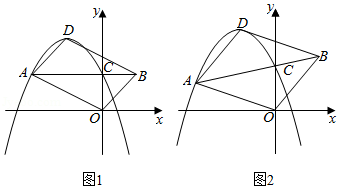
如图,已知在平面直角坐标系 中,抛物线 的顶点为 ,与 轴的交点为 .过点 的直线 与抛物线交于另一点 (点 在对称轴左侧),点 在 的延长线上,连结 , , 和 .
(1)如图1,当 轴时,
①已知点 的坐标是 ,求抛物线的解析式;
②若四边形 是平行四边形,求证: .
(2)如图2,若 , ,是否存在这样的点 ,使四边形 是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.
在新修的花园小区中,有一条“Z”字形绿色长廊ABCD,如图,AB∥CD,在AB、BC、CD三段绿色长廊上各修建一凉亭E、M、F,且BE=CF,M是BC的中点,E、M、F在一条直线上.若在凉亭M与F之间有一池塘,在用皮尺不能直接测量的情况下,你能知道M与F之间的距离吗?试说明理由.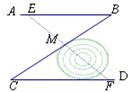
如图,A、B分别表示一骑自行车者和一骑摩托车者在两城镇间旅行时路程与时间的关系,根据这个图像,你能得到关于这两个旅行者在旅行中的哪些信息?(至少写出6个)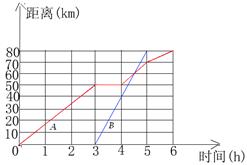
下图是可以自由转动的转盘,该转盘被分成10个相等的扇形.甲、乙两人做如下游戏,并约定:转盘停止转动时,若指针指向偶数区域,则甲获胜;若指针指向奇数区域,则乙获胜.你认为这个游戏对甲、乙双方公平吗?试说明理由.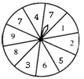
如图,以l为对称轴,画出已知图形的对称图形.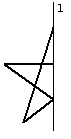
光的速度大约是3×10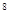 m/s,求光经过7.8×10
m/s,求光经过7.8×10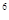 m所需的时间(四舍五入到百分位)
m所需的时间(四舍五入到百分位)