足够长的平行金属导轨MN和PQ表面粗糙,与水平面间的夹角370,间距为1.0m,动摩擦因数为0.25。垂直于导轨平面向上的匀强磁场磁感应强度为4.0T,PM间电阻8.0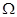 。质量为2.0kg的金属杆ab垂直导轨放置,其他电阻不计。用恒力沿导轨平面向下拉金属杆ab,由静止开始运动,8s末杆运动刚好达到最大速度为8m/s,这8s内金属杆的位移为48m,(g=10m/s2,cos370=0.8,sin370=0.6)
。质量为2.0kg的金属杆ab垂直导轨放置,其他电阻不计。用恒力沿导轨平面向下拉金属杆ab,由静止开始运动,8s末杆运动刚好达到最大速度为8m/s,这8s内金属杆的位移为48m,(g=10m/s2,cos370=0.8,sin370=0.6)
求: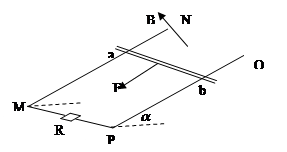
(1)金属杆速度为4.0m/s时的加速度大小。
(2)整个系统在8s内产生的热量。
图(
)所示的
平面处于匀强磁场中,磁场方向与
平面(纸面)垂直,磁感应强度
随时间
变化的周期为
,变化图线如图(
)所示。当
为+
时,磁感应强度方向指向纸外。在坐标原点
有一带正电的粒子
,其电荷量与质量之比恰好等于 。不计重力。设
在某时刻
以某一初速度沿
轴正方向自O点开始运动,将它经过时间
到达的点记为
。
。不计重力。设
在某时刻
以某一初速度沿
轴正方向自O点开始运动,将它经过时间
到达的点记为
。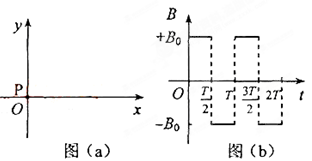
(1)若
=0,则直线
轴的夹角是多少?
(2)若
,则直线
轴的夹角是多少?
(3)为了使直线
轴的夹角为
,在
的范围内,
应取何值?是多少?
如图,在竖直平面内有一固定光滑轨道,其中
是长为R的水平直轨道,
是圆心为
、半径为
的
圆弧轨道,两轨道相切于
点。在外力作用下,一小球从
点由静止开始做匀加速直线运动,到达
点时撤除外力。已知小球刚好能沿圆轨道经过最高点
,重力加速度为
。求: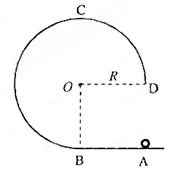
(1)小球在
段运动的加速度的大小;
(2)小球从
点运动到
点所用的时间。
如图所示,AB为竖直半圆轨道的竖直直径,轨道半径R="0.5" m。轨道A端与水平面相切。光滑小球从水平面以初速度v0向A滑动,取g="10" m/s2。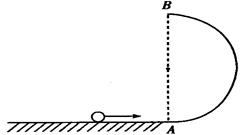
(1)若小球经B点时,对轨道的压力恰好为零,求小球落在水平面时到A点的距离。
(2)若小球在B点的速度VB=4m/s,求小球经A点的瞬间对圆轨道的压力。
2008年9月,神舟七号载人航天飞行获得了圆满成功,我国航天员首次成功实施空间出舱活动、飞船首次成功实施释放小伴星的实验,实现了我国空间技术发展的重大跨越.已知飞船在地球上空的圆轨道上运行时离地面的高度为h.地球半径为R,地球表面的重力加速度为g.求飞船在该圆轨道上运行时速度v的大小和周期T.
如图所示,光滑1/4圆弧的半径为0.8m,有一质量为1.0kg的物体自A点从静止开始下滑到B点,然后沿水平面前进4.0m,到达C点停止。g取10m/s2,求: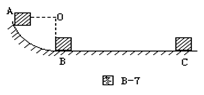
(1)物体到达B点时的速率。
(2)在物体沿水平面运动的过程中摩擦力做的功。