(16分)如图所示,固定的光滑金属导轨间距为L,导轨电阻不计,上端a、b间接有阻值为R的电阻,导轨平面与水平面的夹角为θ,且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中。质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上。初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0。整个运动过程中导体棒始终与导轨垂直并保持良好接触。已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行。
⑴求初始时刻通过电阻R的电流I的大小和方向;
⑵当导体棒第一次回到初始位置时,速度变为v,求此时导体棒的加速度大小a;
⑶导体棒最终静止时弹簧的弹性势能为Ep,求导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q。
如图所示,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,求: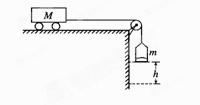
(1)下落过程中绳子的拉力大小;
(2)小桶下落h时的速度大小。
如图,人重600牛,木块A重400牛,人与A、A与地面间的动摩擦因数均为0.2,现人用水平力拉绳,使他与木块一起向右匀速直线运动,滑轮摩擦不计,求(1)人对绳的拉力.(2)人脚给A的摩擦力方向和大小。
2010·全国卷Ⅰ·24汽车由静止开始在平直的公路上行驶,0 ~60s内汽车的加速度随时/间变化的图线如右图所示。
⑴画出汽车在0~60s内的v-t图线;
⑵求在这60s内汽车行驶的路程。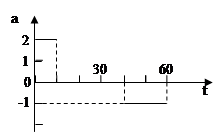
如图所示,质量为m,横截面为直角形的物快ABC,∠ABC=α,AB边靠在竖直墙上,F是垂直于斜面BC的推力,现物块静止不动,求摩擦力的大小。
如图所示,足够长的传送带与水平面倾角θ=37°,以12米/秒的速率逆时针转动。在传送带底部有一质量m = 1.0kg的物体,物体与斜面间动摩擦因数μ= 0.25,现用轻细绳将物体由静止沿传送带向上拉动,拉力F = 10.0N,方向平行传送带向上。经时间t = 4.0s绳子突然断了,(设传送带足够长)求:
(1)绳断时物体的速度大小;
(2)绳断后物体还能上行多远;
(3)从绳断开始到物体再返回到传送带底端时的运动时间。(g = 10m/s2,sin37°= 0.6,cos37°= 0.8,)