（本小题满分14分）函数
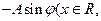
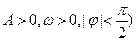的图象在y轴右侧的第一个最高点（即函数取得最大值的点）为
，在原点右侧与x轴的第一个交点为Q（
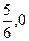）. 求：（1）函数
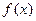的表达式；（2）函数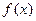在区间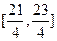
上的对称轴的方程.
（坐标系与参数方程）已知直线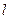
的参数方程：
（
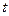为参数）和圆
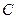的极坐标方程：
（
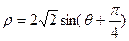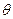为参数）．（1）将直线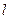的参数方程和圆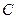的极坐标方程化为直角坐标方程；（2）判断直线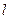和圆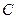的位置关系．
（几何证明选讲）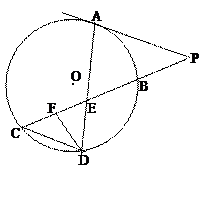
如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF·EC.
(1)求证：ÐP=ÐEDF；
(2)求证：CE·EB=EF·EP；
(3)若CE : BE="3" : 2，DE=6，EF= 4，求PA的长.
(本小题满分10分) 求曲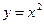线
与直线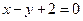
围成图形的面积.
某商品,根据以往资料统计,顾客采用的付款期数
的分布列为
|
1 |
2 |
3 |
4 |
5 |
 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．
表示经销一件该商品的利润．（1）求事件
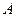：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率
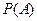；（2）求的分布列及期望
．
的解集;
，求证：
.