已知函数f(x)=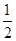 sin2xsinφ+cos2xcosφ-
sin2xsinφ+cos2xcosφ-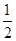 sin
sin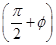 (0<φ<π),其图象过点
(0<φ<π),其图象过点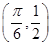 .
.
(1)求φ的值;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的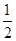 ,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在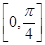 上的最大值和最小值.
上的最大值和最小值.
(本题满分16分)已知函数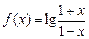 .
.
(1)判断并证明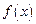 的奇偶性;
的奇偶性;
(2)求证: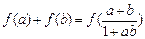 ;
;
(3)已知a,b∈(-1,1 ),且
),且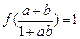 ,
,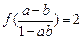 ,求
,求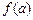 ,
,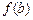 的值.
的值.
(本题满分16分)函数 (
(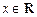 ).
).
(1)求函数 的值域;
的值域;
(2)判断并证明函数 的单调性;
的单调性;
(3)判断并证明函数 的奇偶性;
的奇偶性;
(4)解不等式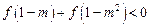 .
.
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次.若每日来回的次数是车头每次拖挂车厢节数的一次函数,每节车厢能载乘客110人.问这列火车每天来回多少次才能使运营人数最多?并求出每天最多运营人数.
计算:
⑴ ;(2)
;(2) .
.
设集合A={x| },B={x|
},B={x| 或
或 }.分别求满足下列条件的实数m的取值范围:
}.分别求满足下列条件的实数m的取值范围:
(1) ;
;
(2) .
.