如图,PDCE为矩形,ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=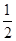 CD=1,PD=
CD=1,PD=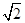 .
.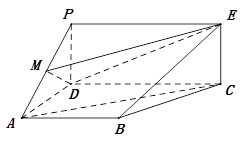
(1)若M为PA中点,求证:AC∥平面MDE;
(2)求直线PA与平面PBC所成角的正弦值;
(3)在线段PC上是否存在一点Q(除去端点),使得平面QAD与平面PBC所成锐二面角的大小为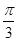 ?
?
选修4—4:坐标系与参数方程
已知直线的极坐标方程为 ,
,
圆 的参数方程为
的参数方程为 .
.
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
选修4-1:几何证明选讲
如图,已知 是⊙
是⊙ 的切线,
的切线,  为切点,
为切点, 是⊙O的割线,与⊙
是⊙O的割线,与⊙ 交于
交于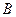 ,
, 两点,圆心
两点,圆心 在
在 的内部,点
的内部,点 是
是 的中点.
的中点.
(1)求证: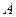 ,
, ,
, ,
, 四点共圆;
四点共圆;
(2)求 的大小.
的大小.
设函数 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)若 的解集;
的解集;
(2)若 上的最小值为
上的最小值为 ,
,
求 的值.
的值.
已知函数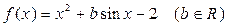 ,
, 且
且 是偶函数.
是偶函数.
(1)求函数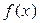 的解析式;
的解析式;
(2)已知函数 在区间
在区间 上单调,
上单调,
求实数 的取值范围.
的取值范围.
已知数列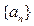 是首项为1的等差数列,其公差
是首项为1的等差数列,其公差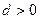 ,且
,且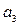 ,
,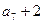 ,
,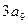 成等比数列.
成等比数列.
(1)求数列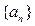 的通项公式;
的通项公式;
(2)设数列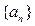 的前n项和为
的前n项和为 ,求
,求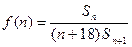 的最大值.
的最大值.