在 中,
中, 分别是三内角
分别是三内角 对应的三边,已知
对应的三边,已知 .
.
(1)求角 的大小;
的大小;
(2)若 ,判断
,判断 的形状.
的形状.
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是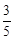 ,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
,乙能答对其中5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,至少得15分才能入选.
(1)求乙得分的分布列和数学期望;
(2)求甲、乙两人中至少有一人入选的概率.
已知 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.
(1)若 ,求
,求 的面积;
的面积;
(2)若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
已知关于x的不等式 (其中
(其中 ).
).
(1)当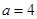 时,求不等式的解集;
时,求不等式的解集;
(2)若不等式有解,求实数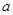 的取值范围
的取值范围
在平面直角坐标系中,曲线C1的参数方程为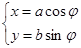 (a>b>0,
(a>b>0,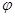 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M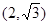 对应的参数
对应的参数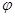 =
=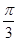 ,
, 与曲线C2交于点D
与曲线C2交于点D
(1)求曲线C1,C2的方程;
(2)A(ρ1,θ),Β(ρ2,θ+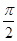 )是曲线C1上的两点,求
)是曲线C1上的两点,求 的值。
的值。
已知PQ与圆O相切于点A,直线PBC交圆于B、C两点,D是圆上一点,且AB∥CD,DC的延长线交PQ于点Q.
求证:
若AQ=2AP,AB= ,BP=2,求QD.
,BP=2,求QD.