李云靠窗坐在一列时速 60千米的火车里，看到一辆有 30节车厢的货车迎面驶来，当货车车头经过窗口时，他开始计时，直到最后一节车厢驶过窗口时，所计的时间是18秒．已知货车车厢长15.8米，车厢间距1.2 米，货车车头长10米．问货车行驶的速度是多少？
如图，线段AD=18cm，线段AC=BD=12cm，E、F分别是线段AB、CD的中点，求线段EF的长．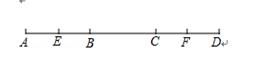
如图所示，∠AOB=∠AOC=90°，∠DOE=90°，OF平分∠AOD，∠AOE=36°．
（1）求∠COD的度数；
（2）求∠BOF的度数．
（1）计算：（﹣3）3÷2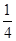
×（﹣
）2+4﹣22×（﹣
）．
（2）先化简，后求值：3a+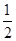
（a﹣2b）﹣（3a﹣6b），其中a=2，b=﹣3．
为了探究n条直线能把平面最多分成几部分，我们从最简单的情形入手：
（1）一条直线把平面分成2部分；
（2）两条直线最多可把平面分成4部分；
（3）三条直线最多可把平面分成11部分…；
把上述探究的结果进行整理，列表分析：
| 直线条数 |
把平面分成部分数 |
写成和形式 |
| 1 |
2 |
1+1 |
| 2 |
4 |
1+1+2 |
| 3 |
7 |
1+1+2+3 |
| 4 |
11 |
1+1+2+3+4 |
| … |
… |
… |
（1）当直线条数为5时，把平面最多分成部分，写成和的形式；
（2）当直线为n条时，把平面最多分成部分．
一个瓶子中装有一些豆子，不用数数的方法，还有几种方法估计瓶中豆子的数目？请写出至少两种方法．