某停车场有10辆出租汽车,第一辆出租汽车出发后,每隔4分钟,有一辆出租汽车开出.在第一辆出租汽车开出2分钟后,有一辆出租汽车进场.以后每隔6分钟有一辆出租汽车回场.回场的出租汽车,在原有的10辆出租汽车之后又依次每隔4分钟开出一辆,问:从第一辆出租汽车开出后,经过多少时间,停车场就没有出租汽车了?
如图,在四边形 中, 是对角线 的中点,连接 并延长交边 于点 .
(1)当点 在 上,①求证: ;②若 ,求 的值;
(2)若 ,求 的长.
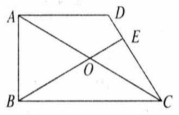
如图,已知圆内接四边形 的对角线 交于点 ,点 在对角线 上,且满足 .求证:
(1) 为 的中点;
(2) .
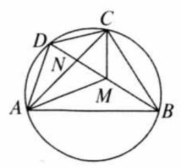
如图, 是钝角三角形, 是 的外接圆,直径 恰好经过 的中点 与 的交点为 为过点 圆的切线,作 也为圆的直径.
(1)求证: ;
(2)已知 的半径为 ,求 的值.

如图所示, 是 的一条弦, 是 外一点, 切 于点 , 交 于点 ,且 于点 是 的中点,求证: .
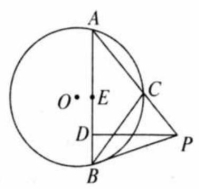
如图,已知 和 相交于 两点,过点 作 的切线交 于点 ,过点 作两圆的割线分别交 于点 与 相交于点 .
(1)求证: ;
(2)求证: ;
(3)当 与 为等圆时,且 时,求 与 的面积的比值.
