已知圆
和点
．
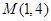（1）过点M向圆O引切线，求切线的方程；
（2）求以点M为圆心，且被直线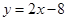
截得的弦长为8的圆M的方程；
（3）设P为（2）中圆M上任意一点，过点P向圆O引切线，切点为Q，试探究：平面内是否存在一定点R，使得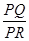
为定值？若存在，请求出定点R的坐标，并指出相应的定值；若不存在，请说明理由．
一个几何体的三视图如下图所示（单位：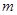
），
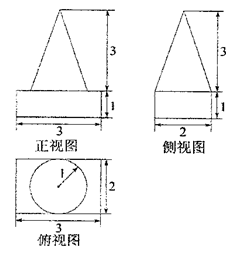
（1）该几何体是由那些简单几何体组成的；
（2）求该几何体的表面积和体积．
已知函数f(x)＝m－|x－2|，m∈R，且f(x＋2)≥0的解集为[－1,1]．
（1）求m的值；
（2）若a，b，c∈R＋，且
＋
＋
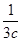＝m，求证：a＋2b＋3c≥9.
已知曲线
的极坐标方程是
，以极点为原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数）.
（Ⅰ）写出直线
的普通方程与曲线的直角坐标方程；
（Ⅱ）设曲线经过伸缩变换
得到曲线
，设
为曲线上任一点，求
的最小值，并求相应点
的坐标.
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=
ACAE=
AB,BD,CE相交于点F.
（Ⅰ）求证:A,E,F, D四点共圆；
（Ⅱ）若正△ABC的边长为2,求A,E,F,D所在圆的半径.
已知函数
（k为常数，e=2.71828……是自然对数的底数），曲线
在点
处的切线与x轴平行。
（1）求k的值；
（2）求
的单调区间；
（3）设
，其中
为的导函数，证明：对任意
，
。