已知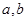 为正整数(
为正整数(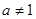 ),等差数列
),等差数列 的首项为
的首项为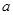 ,公差为
,公差为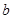 , 等比数列
, 等比数列 的首项为
的首项为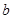 ,公比为
,公比为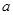 .满足条件
.满足条件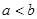 ,且
,且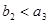 .在数列
.在数列 与
与 中各存在一项
中各存在一项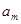 与
与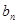 有
有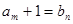 ,又设
,又设 .
.
(1)求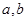 的值.
的值.
(2)若数列 为等差数列,求常数
为等差数列,求常数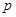 .
.
已知 是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合
是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合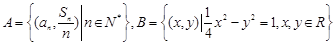 .试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
.试问下列命题是否是真命题,如果是真命题,请给予证明;如果是假命题,请举反例说明.
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2) 至多有一个元素;
至多有一个元素;
(3)当a1≠0时,一定有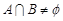 .
.
写出下列命题的逆命题、否命题、逆否命题,并指出他们的真假:
(1)若xy=0,则x,y中至少有一个是0;
(2)若x>0,y>0,则xy>0;
把命题“未位数是0的整数可以被5整除”改写为“若p则q”的形式,并写出它的逆命题、否命题与逆否命题
等比数列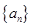 中,
中,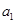 ,
, ,
,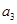 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且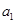 ,
, ,
,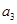 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| 第一列 |
第二列 |
第三列 |
|
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ)求数列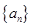 的通项公式;
的通项公式;
(Ⅱ)若数列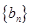 满足:
满足: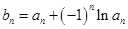 ,求数列
,求数列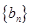 的前
的前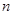 项和
项和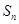 .
.
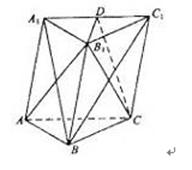
如图,棱柱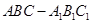 的侧面
的侧面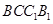 是菱形,
是菱形,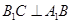 .
.
(Ⅰ)证明:平面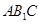
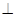 平面
平面 ;
;
(Ⅱ)设 是
是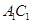 上的点,且
上的点,且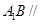 平面
平面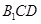 ,求
,求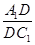 的值.
的值.