某品牌的饼干袋里,装有动物、笑脸、数字三种花纹的饼干(除花纹外其余都相同),其中有动物花纹饼干2个,笑脸花纹饼干1个,数字花纹饼干若干个,现从中任意拿出一个饼干是动物花纹的概率为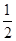 .
.
(1)求口袋中数字饼干的个数;
(2)小亮同学先随机拿出一个饼干吃掉,又随机拿出一个饼干吃掉,请用“树状图法”或“列表法”,求两次吃到的都是动物花纹饼干的概率.
(1)问题
如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
(2)探究
如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用
请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以D为圆心,以DC为半径的圆与AB相切,求t的值.
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,销售单价应定为多少?
如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.
(1)判断△ABC的形状:;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.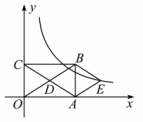
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度.小明为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.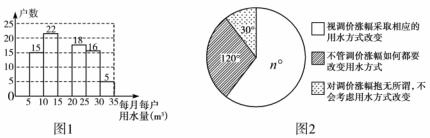
小明发现每月每户的用水量在5m2-35m2之间,有8户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)n=,小明调查了户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在的小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?