吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图: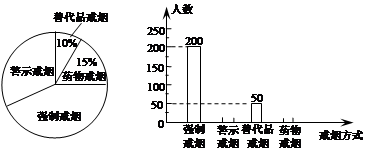
根据统计图解答下列问题:
(1)同学们一共调查了 人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。在(3)的条件下,若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
如图, 已知抛物线 与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
与x轴相交于A、B,点B的坐标为(10,0),顶点M的坐标为(4,8),点P从点M出发,以每秒1个单位的速度沿线段MA向A点运动;点Q从点A出发,以每秒2个单位的速度沿AB向B点运动,若P、Q同时出发,当其中的一点到达终点时,另一点也随之停止运动,设运动时间为t秒钟。
(1)求抛物线的解析式;
(2)设△APQ的面积为S,求S与t之间的函数关系式,△APQ的面积是否有最大值?若有,请求出其最大值;若没有,请说明理由;
(3)当t为何值时,△APQ为等腰三角形?
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题:
(1)求 与
与 的关系式;
的关系式;
(2)当 取何值时,
取何值时, 的值最大?
的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?
如图3,在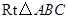 中,
中,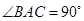 ,
,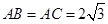 ,
, 两点分别在
两点分别在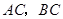 上,
上,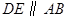 ,
,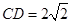 ,将
,将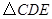 绕点
绕点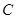 顺时针旋转,得到
顺时针旋转,得到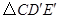 (如图4,点
(如图4,点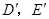 分别与
分别与 对应),点
对应),点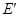 在
在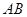 上,
上,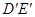 与
与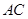 相交于点
相交于点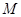 .
.
(1)求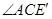 的度数;
的度数;
(2)求证:四边形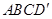 是梯形;
是梯形;
(3)求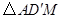 的面积.
的面积.
如图,在平面直角坐标系中,坐标原点为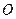 ,
,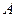 点坐标为
点坐标为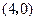 ,
,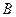 点坐标为
点坐标为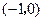 ,以
,以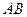 的中点
的中点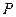 为圆心,
为圆心,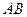 为直径作⊙P与
为直径作⊙P与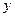 轴的正半轴交于点
轴的正半轴交于点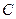 .
.
(1)求经过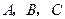 三点的抛物线对应的函数表达式.
三点的抛物线对应的函数表达式.
(2)设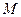 为(1)中抛物线的顶点,求直线
为(1)中抛物线的顶点,求直线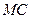 对应的函数表达式.
对应的函数表达式.
(3)试说明直线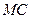 与⊙P的位置关系,并证明你的结论.
与⊙P的位置关系,并证明你的结论.
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为
形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为 ,宽为
,宽为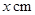 ,分别回答下列问题:
,分别回答下列问题: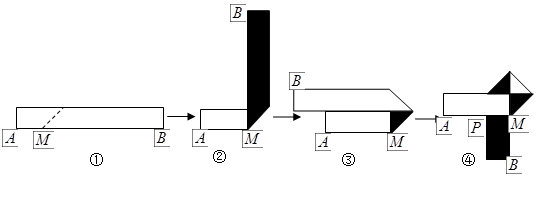
(1)为了保证能折成图④的形状(即纸条两端均超出点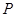 ),试求
),试求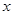 的取值范围.
的取值范围.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点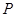 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点
的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点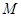 与点
与点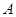 的距离(用
的距离(用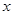 表示)
表示)