列方程或方程组解应用题:
为保证“燕房线”轻轨建设,我区对一条长2 500米的道路进行改造.在改造了1 000米后,为了减少施工对交通造成的影响,采用了新的施工工艺,使每天的工作效率是原来的1.5倍,结果提前5天完成任务.求原来每天改造道路多少米?
求如图所示的RtΔABC的面积。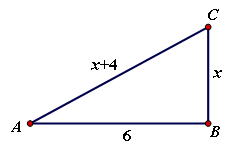
(1)如图1,已知△ABC,以边AB、AC为边分别向外作等边三角形ABD和等边三角形ACE,连接CD、BE.求证:⑴CD=BE.
(2)如图2,已知△ABC,以边AB、AC为边分别向外作正方形ABFD和正方形ACGE,连接CD、BE,CD与BE有什么数量关系?(直接写结果,不需要过程).
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.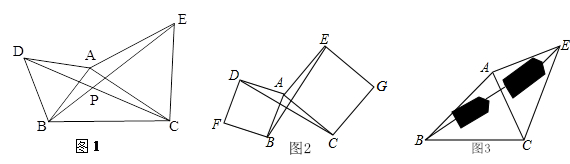
某市现有两种用电收费方法:
| 分时电表 |
普通电表 |
|
| 峰时(8:00—21:00) |
谷时(21:00到次日8:00) |
电价0.52元/度 |
| 电价0.55元/度 |
电价0.35元/度 |
小明家所在的小区的电表都换成了分时电表,根据情况回答下列问题:
(1)第一季度小明家用电情况为:谷时用电量100度,峰时用电量300度,这个季度的费用和用普通电表收费相比,哪种收费方法合算?试说明理由.
(2)一月份小明家用电100度,那么小明家使用分时电表是不是一定比普通电表合算?试说明理由.
如图,△ABC为等边三角形,E为AC上一点,连接BE,将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,点E落在点C处,连接AF.求证:四边形ABDF为平行四边形.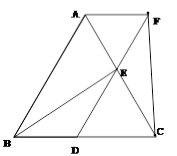
某文具店老板第一次用1000元购进一批文具,很快销售完毕,第二次购进时发现每件文具的进价比第一次上涨了2.5元,老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快销售完毕,已知两批文具的售价均为每件15元.
(1)第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?