以 的两边 、 为边,向外作正方形 和正方形 ,连接 ,过点 作 于 ,延长 交 于点 .
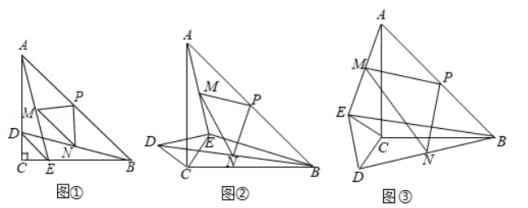
( 1 )如图 1 ,若 , ,易证: ;
( 2 )如图 2 , ;如图 3 , ,( 1 )中结论,是否成立,若成立,选择一个图形进行证明;若不成立,写出你的结论,并说明理由.
为抗击疫情,支持武汉,某物流公司的快递车和货车每天往返于物流公司、武汉两地,快递车比货车多往返一趟,如图表示两车离物流公司的距离 (单位:千米)与快递车所用时间 (单位:时)的函数图象,已知货车比快递车早 小时出发,到达武汉后用 小时装卸货物,按原速、原路返回,货车比快递车最后一次返回物流公司晚 小时.
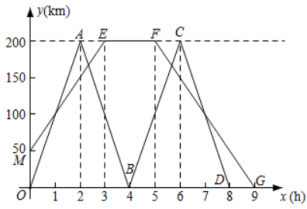
( 1 )求 的函数解析式;
( 2 )求快递车第二次往返过程中,与货车相遇的时间.
( 3 )求两车最后一次相遇时离武汉的距离.(直接写出答案)
某公司工会组织全体员工参加跳绳比赛,工会主席统计了公司 50 名员工一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).

求:(1) 该公司员工一分钟跳绳的平均次数至少是多少;
(2) 该公司一名员工说:"我的跳绳成绩是我公司的中位数"请你给出该员工跳绳成绩的所在范围;
(3) 若该公司决定给每分钟跳绳不低于 140 个的员工购买纪念品,每个纪念品 300 元,则公司应拿出多少钱购买纪念品.
如图,已知二次函数 与 轴交于 、 两点(点 位于点 的左侧),与 轴交于点 ,已知 的面积是 6 .
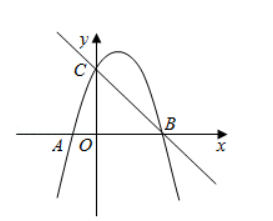
( 1 )求 的值;
( 2 )在抛物线上是否存在一点 ,使 .存在请求出 坐标,若不存在请说明理由.
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中, 的三个顶点 、 、 均在格点上

( 1 )将 向左平移 个单位得到 ,并写出点 的坐标;
( 2 )画出 绕点 顺时针旋转 后得到的 ,并写出点 的坐标;
( 3 )在( 2 )的条件下,求 在旋转过程中扫过的面积(结果保留 ).