某步行街摆放有若干盆甲、乙、丙三种造型的盆景.甲种盆景由15朵红花、24朵黄花和25朵紫花搭配而成;乙种盆景由10朵红花、12朵黄花搭配而成;丙种盆景由10朵红花、18朵黄花和25朵紫花搭配而成.这些盆景一共用了2900朵红花,3750朵紫花,则黄花一共用了 朵.
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是m(可利用的围墙长度超过6m).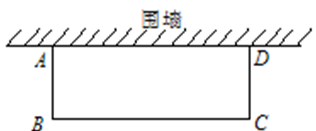
如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD=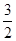 ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.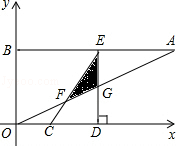
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有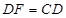 ?
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
在如图的直角坐标系中,已知点A(2,0)、B(0,-4),将线段AB绕点A按逆时针方向旋转90°至AC.
(1)求点C的坐标;
(2)若抛物线y=-x2+ax+4经过点C.
①求抛物线的解析式;
②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F.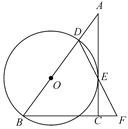
(1)求证:DE=FE;
(2)若BC=9,AD=6,求BF的长.
认真观察图1的4个图中阴影部分构成的图案,回答下列问题:

(1)请写出这四个图案都具有的两个共同特征.
特征1:;特征2:.
(2)请在图2中设计出你心中的图案,使它也具备你所写出的上述两个特征.