如图，在平面直角坐标系xOy中，点A、B坐标分别为（4，2）、（0，2），线段CD在于x轴上，CD＝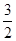
，点C从原点出发沿x轴正方向以每秒1个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E、交OA于点G，连结CE交OA于点F．设运动时间为t，当E点到达A点时，停止所有运动．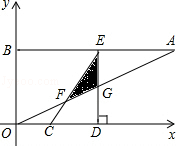
（1）求线段CE的长；
（2）记S为RtΔCDE与ΔABO的重叠部分面积，试写出S关于t的函数关系式及t的取值范围；
（3）连结DF，
①当t取何值时，有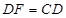
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
用反证法证明“三角形的三个内角中，至少有一个内角小于或等于60°”
证明：假设所求证的结论不成立，即
∠A 60°，∠B60°，∠C60°,
则∠A+∠B+∠C ＞ 。
这与相矛盾。
∴不成立。
∴。
为了降低能源消耗，减少环境污染，国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”，并从2008年6月1日起正式实施．某中学八年级共有400名学生。学校为了增强学生的环保意识，在本年级进行了一次环保知识测验．为了了解这次测验的成绩状况，从中抽取了50名学生的成绩，将所得数据整理后，画出频数分布直方图如图所示．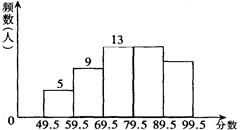
(1)第五个小组的频数和频率各是多少?
(2) 这50名学生的成绩的中位数在哪一组?
(3)这次测验中，八年级全体学生成绩在59.5～69.5 中的人数约是多少?
选择适当方法解方程：
①x2＝3x②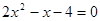
△ABC中，AB=1,AC=2,D是BC中点,AE平分∠BAC交BC于E,且DF∥AE.求CF的长.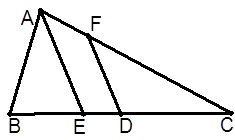
已知抛物线y=ax2+bx+c ，当x=0时，有最小值为1 ；且在直线y=2上截得的线段长为4 .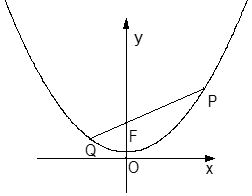
（1）求此抛物线的解析式；
（2）若点P是抛物线的任意一点，记点P到X轴的距离为d1，点P 与点 F （0，2）的距离为d 2，猜想d1、 d 2的大小关系，并证明；
（3）若直线PF交此抛物线于另一点Q（异于P点）。 试判断以PQ为直径的圆与x 轴的位置关系，并说明理由。