对任意函数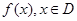 ,可按流程图构造一个数列发生器,其工作原理如下:①输入数据
,可按流程图构造一个数列发生器,其工作原理如下:①输入数据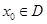 ,数列发生器输出
,数列发生器输出 ;②若
;②若 ,则数列发生器结束工作;若
,则数列发生器结束工作;若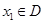 ,则将
,则将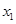 反馈回输入端再输出
反馈回输入端再输出 ,并且依此规律继续下去.现定义
,并且依此规律继续下去.现定义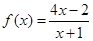 .
.
(1)若输入 ,则由数列发生器产生数列
,则由数列发生器产生数列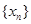 ,请写出数列
,请写出数列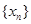 的所有项;
的所有项;
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据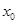 的值;
的值;
(3)若输入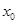 时,产生的无穷数列
时,产生的无穷数列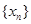 满足:对任意正整数
满足:对任意正整数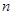 ,均有
,均有 ,求
,求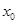 的
的
取值范围.
(本小题满分l 2分)某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x元时,销售量可达到15一O.1x万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价 格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
(I)每套丛 书定价为100元时,书商能获得的总利润是多少万元?
书定价为100元时,书商能获得的总利润是多少万元?
(Ⅱ)每套丛书定价为多少元时,单套丛书的利润最大?
.(本小题满分1 2分)设△ABC的内角A 、B、C所对的边分别为a、b、c.已知a=3,B=
、B、C所对的边分别为a、b、c.已知a=3,B= ,S△ABC=6
,S△ABC=6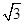
( I )求△ABC的周长;
(Ⅱ)求sin2A的值 .
.
(本小题满分12分)已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子 里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(I)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性
最大?请说明理由. ’
.(本小题满分l 2分) 已知{an}是等比数列,a1=2,且a1,a3+1,a4成等差数列.
(I)求数列{a n}的通项公式;
(Ⅱ)若bn=log2 an,求数列{bn}的前n项和Sn.
(本小题满分12分)证明函数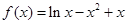 只有一个零点.
只有一个零点.